Pojęcie nieskończoności już od czasów starożytnej Grecji było tematem dyskusji i wzbudzało wiele kontrowersji, bo prowadziło do paradoksów. Jeden z nich opisałem w artykule „Achilles goni żółwia”.
Podstawowym pytaniem dotyczącym nieskończoności było to czy ona istnieje w rzeczywistości (za Arystotelesem możemy ją nazwać „rzeczywistą”) czy też jest tylko możliwością powtarzania jakiegoś działania bez ograniczeń (za Arystotelesem możemy ją nazwać „potencjalną”).
Nieskończoność „rzeczywista” oznacza, że istnieje obiekt, który ma nieskończenie wiele elementów.
Nieskończoność „potencjalna” oznacza, że możemy bez końca dzielić jakiś obiekt na coraz mniejsze części.
Zacznijmy od dziedziny, w której obie nieskończoności – „rzeczywista” i „potencjalna” istnieją, co więcej są niezbędne. Tą dziedziną jest matematyka.
Rozważmy najprostszy przykład. Liczb naturalnych, czyli 1,2,3 … , jest nieskończenie wiele. Wynika to z prostego rozumowania. Gdyby tak nie było, to musiałaby istnieć największa liczba naturalna. Do tej liczby moglibyśmy dodać jeden i uzyskać liczbę większą od tej największej. Ta większa też nie jest największa, bo możemy dodać do niej jeden i tak bez końca. Zatem nie istnieje największa liczba naturalna co oznacza, że liczb tych jest nieskończenie wiele. Liczba elementów, z których składa się zbiór nazywana jest w matematyce mocą zbioru. Zbiór liczb naturalnych ma więc nieskończoną liczbę elementów więc jego moc jest nieskończona.
Pojęcie nieskończoność kryje jednak w sobie zadziwiające własności, które sprawiają, że zawodzi nas intuicyjne rozumienie tego pojęcia.
Część jest tak samo duża jak całość
Przyjrzyjmy się pierwszej zadziwiającej własności. Załóżmy, że utworzymy zbiór złożony tylko z niektórych liczb naturalnych. Do tego zbioru wybieramy tylko liczby parzyste.
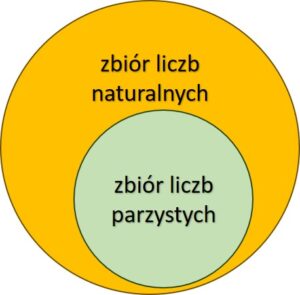
Zbiór liczb parzystych jest częścią zbioru liczb naturalnych
Możemy teraz utworzyć pary w ten sposób, że każda para będzie zawierać liczbę naturalną i liczbę parzystą. Przy tworzeniu kolejnych par nigdy nie zabraknie nam ani liczby naturalnej ani liczby parzystej. Oznacza to, że oba zbiory mają taką samą liczbę elementów, czyli moce obu tych zbiorów są takie same.
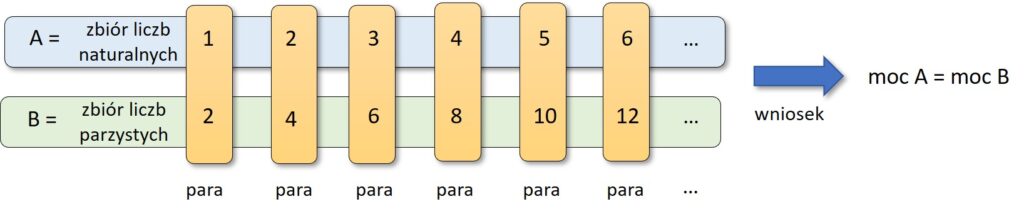
Łączenie w pary liczb naturalnych i liczb parzystych pokazuje, że moce obu zbiorów są równe
Zadziwiające, bo przecież pierwszy zbiór zawiera zarówno liczby parzyste jak i nieparzyste a drugi tylko parzyste. Wydawałoby się zatem, że ten drugi zbiór powinien być mniej liczny od pierwszego. Tak jednak nie jest !
Suma nieskończonej liczby liczb może być skończona
Druga niezwykła własność ma związek z sumowaniem liczb. Kiedy sumujemy nieskończoną liczbę liczb, to wydawać by się mogło, że taka suma będzie miała zawsze nieskończoną wartość. Okazuje się, że suma ta może być zarówno nieskończona jak i skończona. Wynik zależy od tego jakie liczby sumujemy a nie od tego, że jest ich nieskończenie wiele. Przykład takich sumowań podałem w artykule „Achilles goni żółwia”.
![]()
Przykład skończonej sumy nieskończonej liczby składników
Aby zrozumieć dlaczego wartość sumy nieskończonej liczby składników może być skończona spójrzmy na to w ten sposób: bierzemy skończoną liczbę a następnie dzielimy ją na nieskończoną liczbę części.
Różne nieskończoności
Nieskończoność, która jest mocą zbioru liczb naturalnych nie jest jedyną nieskończonością. Jeśli do zbioru liczb naturalnych dodamy liczby wymierne, takie które mają postać ułamka i niewymierne, takie jak liczba π, to otrzymamy zbiór liczb rzeczywistych.
Już sama liczba π jest niezwykła, bo tak jak każda liczba niewymierna, jej rozwinięcie dziesiętne tworzy nieskończenie długi ciąg cyfr, bez powtarzającego się cyklu cyfr. Oznacza to, że nigdy nie zobaczymy jej pełnego rozwinięcia dziesiętnego, bo żeby to zrobić musielibyśmy zużyć nieskończenie wiele czasu i mieć nieskończenie długi arkusz papieru. Dlatego do oznaczenia tej liczby stosujemy symbol literowy.
Oto pierwsze 45 cyfr z nieskończonego rozwinięcia dziesiętnego liczby π
π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 …
Liczb rzeczywistych jest także nieskończenie wiele, ale ta nieskończoność jest zupełnie inna niż nieskończoność zbioru liczb naturalnych. Zobaczmy dlaczego.
Modelem geometrycznym liczb rzeczywistych jest prosta o nieskończonej długości. Każdy punkt na prostej oznacza jedną liczbę rzeczywistą. Liczby naturalne, które są podzbiorem liczb rzeczywistych, tworzą na prostej zbiór punktów równo oddalonych od siebie.
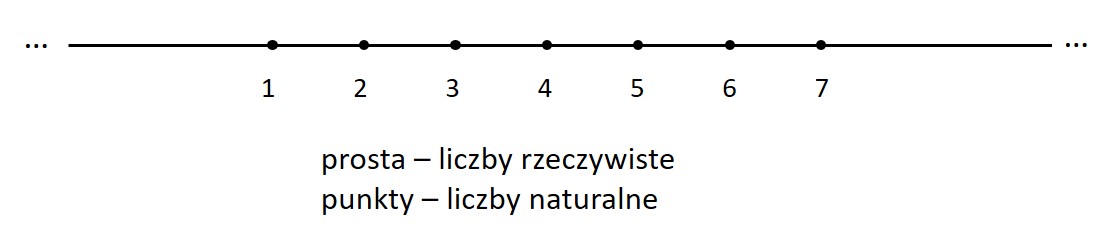
Nieskończona prosta – model liczb rzeczywistych
Jeżeli weźmiemy dwie sąsiednie liczby naturalne, takie które różnią się o jeden, to między tymi liczbami nie ma żadnej innej liczby naturalnej. Oznacza to, że możemy „ustawić” liczby naturalne w szereg, w którym każda następna liczba jest większa od poprzedniej o jeden.
Spróbujmy postąpić podobnie z liczbami rzeczywistymi. Jeśli nam się to uda, to znaczy, że moce zbioru liczb rzeczywistych i liczb naturalnych będą równe.
Weźmy więc dwa różne punkty na osi liczbowej, czyli dwie różne liczby rzeczywiste. Okazuje się, że bez względu na odległość tych punktów, liczb rzeczywistych pomiędzy nimi będzie nieskończenie wiele. Możemy zmniejszać odległość pomiędzy punktami, ale bez względu na to jak mała będzie ta odległość, nigdy nie dojdziemy do takiej sytuacji, aby w przedziale zostały tylko dwie liczby rzeczywiste. Zawsze pomiędzy tymi punktami będzie nieskończenie wiele liczb rzeczywistych.
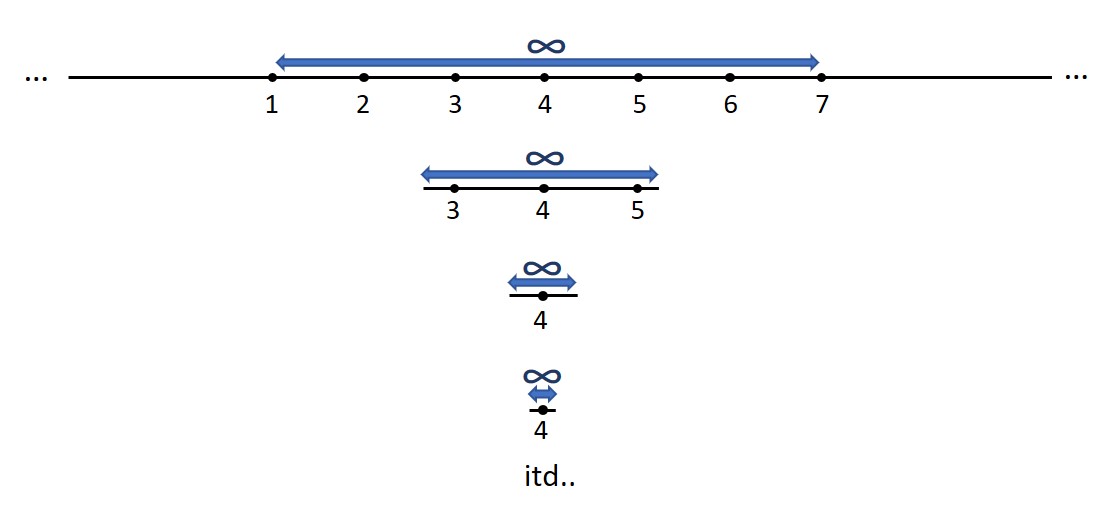
Pomiędzy dwiema liczbami rzeczywistymi jest zawsze nieskończenie wiele liczb rzeczywistych, bez względu na to jak blisko siebie są te dwie liczby
Oznacza to, że nie da się „ustawić” w szereg liczb rzeczywistych, tak aby każda następna była większa od poprzedniej.
Obrazowo można powiedzieć, że liczby rzeczywiste to nieskończenie długa nitka makaronu, na której znajdują się ziarenka maku – liczby naturalne. Bardzo łatwo możemy wyjąć wszystkie ziarenka maku i ustawić je w szereg, bo one oddzielone są od siebie. Nie uda nam się jednak zrobić tego samego z nitką makaronu. Ona ma strukturę ciągłą więc nie sposób wykroić dwóch bezpośrednio sąsiadujących ze sobą drobinek makaronu, bo każdy kawałek makaronu możemy znowu podzielić na dwa mniejsze i tak bez końca.
Okazuje się więc, że nieskończoność liczb rzeczywistych jest nieskończenie większa od nieskończoności liczb naturalnych, czyli moc zbioru liczb rzeczywistych jest większa od mocy zbioru liczb naturalnych.
Jeśli intuicyjnie można wyobrażać sobie nieskończoność liczb naturalnych, to nieskończoność nieskończenie większa od nieskończoności stanowi dla intuicji duże wyzwanie.
Skoro istnieją różne nieskończoności, to nasuwa się pytanie czy istnieją jakieś jeszcze inne rodzaje nieskończoności. Czy istnieje np. taki zbiór, którego moc jest większa od mocy liczb naturalnych, ale mniejsza od mocy liczb rzeczywistych ? Matematyka odpowiada na to pytanie w zadziwiający sposób – zarówno twierdząca jak i przecząca odpowiedź jest możliwa.
Obiekt matematyczny, który przedstawia liczby rzeczywiste, czyli prosta, zawiera obie nieskończoności, „rzeczywistą”, bo jej długość jest nieskończona i „potencjalną”, bo można dzielić prostą na coraz mniejsze odcinki nieskończenie wiele razy.
Nieskończoność występuje w wielu działach matematyki i jest niezbędna, aby rozważania matematyczne były możliwe. Rozumienie intuicyjne nieskończoności nie jest tu wymagane. Dotyczy to zresztą nie tylko nieskończoności. Wystarczy przywołać przykład przestrzeni czterowymiarowej, której własności matematyczne są dobrze zdefiniowane, ale której nie potrafimy sobie wyobrazić.
Nieskończoność w realnym świecie
Skoro nieskończoność jest niezbędnym pojęciem matematycznym, to zapytajmy czy nieskończoność istnieje w świecie realnym.
Fizyka opisuje świat poprzez teorie fizyczne, a matematyka jest językiem teorii. Skoro w matematyce pojawia się nieskończoność, to musi się także pojawić w fizyce. W odróżnieniu jednak od matematyki, gdzie o poprawności twierdzenia decyduje dowód, twierdzenia fizyczne muszą zostać potwierdzone doświadczalnie. Zgodność z doświadczeniem jest jedynym kryterium poprawności teorii.
Kłopot fizyki polega na tym, że nieskończoność pojawia się w teoriach, ale jak dotąd żadne doświadczenia nie potwierdziły istnienia nieskończoności zarówno „rzeczywistej” – żadna wielkość fizyczna nie przyjmuje nieskończonej wartości, jak i „potencjalnej”- nie możemy w nieskończoność dzielić materii, bo po skończonej liczbie kroków, dotrzemy do poziomu atomów a potem cząstek elementarnych. Nieskończoności pojawiają się jednak, i to w wielu miejscach, jako efekt teorii, które stosujemy do opisu rzeczywistości.
Podstawowym założeniem, które prowadzi do nieskończoności jest przyjęcie, że nasza czasoprzestrzeń ma strukturą ciągłą. W języku matematyki oznacza to, że dowolny „kawałek” czasoprzestrzeni możemy bez końca dzielić na coraz mniejsze „kawałki”. Odpowiada to opisanej wcześniej możliwości dzielenia prostej liczb rzeczywistych.
Nieskończoności nie pojawiłyby się gdybyśmy mogli stworzyć teorię opartą na założeniu dyskretności czasoprzestrzeni, w której odległości między punktami byłyby skończone. Niestety jak dotąd nie potrafimy zbudować teorii opartej na takim założeniu.
Można powiedzieć, że fizyka otrzymuje od matematyki nieskończoność jako niechciany prezent. Musi więc jakoś poradzić sobie w tej sytuacji.
Jak fizyka radzi sobie z niechcianą nieskończonością
Fizycy mają sposoby na unikanie nieskończoności.
Sposób 1
Jeśli w wyniku obliczeń pojawiają się nieskończone wielkości, to stosowane są procedury, które sprowadzają się do nieuprawnionego matematycznie odejmowania nieskończoności od nieskończoności w taki sposób, żeby otrzymać wartości skończone, które zgadzają się z doświadczeniem.
Najbardziej niezwykłe jest to, że pomimo tych wątpliwych matematycznie procedur, wyliczone w taki sposób wartości zgadzają się z wartościami obserwowanymi z niezwykłą dokładnością (do kilkunastu miejsc po przecinku).
Takie procedury obliczeniowe przypominają sytuację, w której kucharz pytany o to dlaczego stosowany przez niego przepis jest dobry odpowiada: ”nie wiem, ale stosuję ten przepis, bo uzyskuję wspaniały smak potrawy”.
Sposób 2
Jeśli równania teorii dopuszczają wartości nieskończenie małe lub nieskończenie duże, to wprowadzamy ograniczenia zakresu stosowania tych równań. Innymi słowy przyjmujemy, że równania przestają obowiązywać poniżej lub powyżej pewnych wartości zmiennych, które w nich występują. To tak jakbyśmy powiedzieli, że nie ma sensu konstruować silniejszego mikroskopu lub silniejszego teleskopu, bo nic mniejszego ani nic większego nie zobaczymy.
A może Wszechświat jest nieskończony ?
Wszechświat jest największym układem fizycznym. Obserwujemy tak ogromne skale odległości do gwiazd i galaktyk, że naturalne wydaje się przypuszczenie o jego nieskończonej wielkości. Przypuszczenie to jest jednak na gruncie obecnej fizyki nierozstrzygalne. Innymi słowy równie dobrze możemy założyć, że Wszechświat jest nieskończony jak i że jest skończony. Tyle tylko, że przyjęcie założenia o nieskończoności Wszechświata nie wnosi istotnej wartości do opisu fizycznego. Wynika to z faktu istnienia maksymalnej prędkości rozchodzenia się wszelkich oddziaływań. Tą prędkością jest prędkość światła w próżni.
Skończona prędkość rozchodzenia się oddziaływań oznacza, że obszar który może oddziaływać na obserwatora jest także skończony. Ponieważ oddziaływanie spoza tego obszaru nie dociera do obserwatora, to fakt istnienie tego obszaru jest dla obserwatora nieistotny.
Nawet gdyby okazało się, że istnieje nośnik oddziaływań rozchodzący się z prędkością większą niż światło nie zmieniłoby to faktu, że obszar oddziałujący na obserwatora byłyby wprawdzie większy, ale wciąż skończony.
Zawsze jednak istnieje możliwość pojawienia się takiej teorii, która lepiej niż obecne teorie opisze wszystkie oddziaływania fizyczne i będzie wymagać przyjęcia założenia o nieskończoności Wszechświata. Wtedy nieskończoność Wszechświata byłaby w sposób pośredni potwierdzona, nie przez jego bezpośrednią obserwację, ale poprzez zgodność przewidywań tej teorii z doświadczeniem.
Z podobną sytuacją mamy do czynienia przy próbach wyjaśnienie tempa rozszerzania Wszechświata i ruchu galaktyk. Aby uzyskać opis zgodny z doświadczeniem została przyjęta hipoteza o istnieniu nowych nieznanych wcześniej form materii i energii. Te nowe formy zostały nazwane ciemną materią i ciemną energią. Nazwy wskazują na to, że obu tych stanów nie obserwujemy doświadczalnie i nie wiemy jakie mają własności. Zadziwiające jest także to, że aby wyjaśnić tempo rozszerzania się Wszechświata musimy przyjąć, że ciemna materia i ciemna energia stanowią ponad 90% całkowitej energii Wszechświata więc to co dotychczas obserwujemy jest tylko małym wycinkiem całości. Oczywiście dopóki nie uzyskamy potwierdzenia doświadczalnego ciemna materia i ciemna energia zostaną tylko hipotezą roboczą.
Podstawowym pytaniem jest to jaki model przestrzeni jest właściwy do opisu Wszechświata. To czy pojawi się nieskończoność czy też nie, zależy od tego jaki model przyjmiemy. Pokażę to na przykładzie przestrzeni trójwymiarowych, choć liczba wymiarów modelu jest także otwartą kwestią. Obecnie stosujemy model czterowymiarowy – trzy wymiary przestrzenne i jeden wymiar czasowy. Jest jednak także koncepcja, która zakłada, że zamiast cząstek mamy obiekty zwane strunami. Struny mogą drgać w dodatkowych wymiarach co sprawia, że Wszechświat ma w tej teorii 11 wymiarów.
Oto kilka przykładów przestrzeni trójwymiarowych.
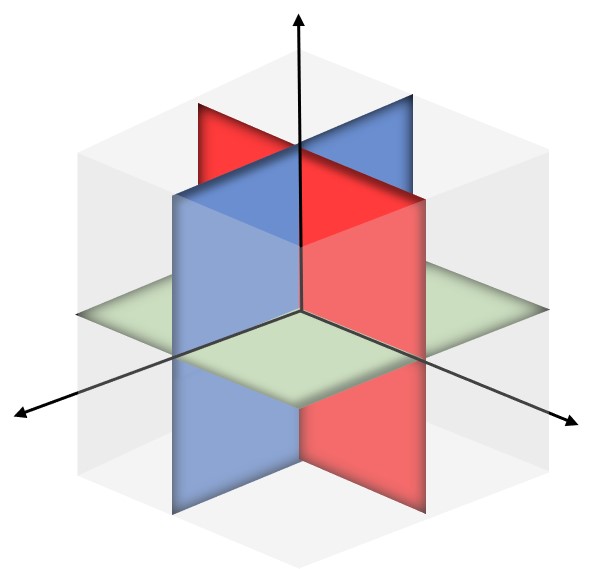
Przestrzeń trójwymiarowa, która rozciąga się w nieskończoność w każdym wymiarze.

Kula – ma skończoną objętość i powierzchnię.

Torus – ma skończoną objętość i powierzchnię.

Walec o nieskończonej długości – ma nieskończoną objętość i powierzchnię.
Warto wspomnieć o bardzo ciekawej przestrzeni, która nosi nazwę rogu Gabriela lub trąbki Torricellego.

Róg Gabriela ma nieskończoną powierzchnię, ale skończoną objętość.
źródło: https://en.wikipedia.org/wiki/Gabriel%27s_horn#/media/File:GabrielHorn.png
Z opisem matematycznej konstrukcji rogu Gabriela można zapoznać się na stronie:
https://pl.wikipedia.org/wiki/R%C3%B3g_Gabriela.
* * *
Podsumowując, istnienie nieskończoności, oczywiste w matematyce, w świecie rzeczywistym jest kwestią otwartą.
Pora zakończyć artykuł, choć nie wyczerpałem tematu, ale nie mogę pisać nieskończenie długo jeśli czytelnik ma skończony czas na lekturę.
Na koniec graficzna sztuczka, która pozwala pozbyć się nieskończoności: wystarczy jej symbol

obrócić o kąt prosty i mamy

skończoną liczbę – osiem, która symbolizuje nowe otwarcie. Może to otwarcie powie nam coś więcej o nieskończoności a może nieskończoność zachowa jednak swoje tajemnice.
***
2024