Achilles goni żółwia

Grecki filozof Zenon z Elei jest autorem kilku paradoksów, z których najbardziej znany jest paradoks pościgu żółwia przez Achillesa. Według Zenona Achilles, mimo że jest szybkobiegaczem nie dogoni wolno poruszającego się żółwia. Rozumowanie jest następujące. Na starcie biegu żółwia i Achillesa dzieli pewien dystans. Jeśli Achilles dobiegnie do punktu, z którego rozpoczął bieg żółw, to żółw zdąży oddalić się od tego punktu. Achilles będzie więc musiał przebyć tę odległość, ale kiedy dotrze do tego punktu, żółw znowu zdąży się oddalić.  Wprawdzie dystans dzielący Achillesa i żółwia będzie się zmniejszał, ale zawsze żółw będzie przez Achillesem. Zatem Achilles nigdy nie dogoni żółwia.

W rzeczywistości Achilles oczywiście dogoni żółwia, ale kwestionując wniosek Zenona należy wykazać dlaczego jego rozumowanie jest błędne.  Różne rozwiązania paradoksu Zenona przedstawiło wielu myślicieli począwszy od Arystotelesa i Archimedesa.

Według mnie kluczowym w paradoksie Zenona jest czas. Wniosek, że Achilles nie dogoni żółwia oznacza, że czas pogoni będzie nieskończony. Zenon rozłożył pościg Achillesa na nieskończona liczbę etapów. Każdy kolejny etap Achilles przebiega wprawdzie w coraz krótszym czasie, ale ponieważ liczba etapów jest nieskończona, to oczywistym wydaje się wniosek, że czas pogoni będzie nieskończony. To jest istota paradoksu.

Zenon doszedł do takiego wniosku ponieważ nie wiedział jak niezwykłym obiektem jest nieskończoność. Nieintuicyjną własność nieskończoności jest fakt, że suma nieskończonej liczby składników nie musi być nieskończona.

Pokażmy to na konkretnym przykładzie.

Załóżmy, że na początku Achillesa i żółwia dzieli 10 m. Achilles porusza się z prędkością 10 m/s (jest przecież sprinterem), a żółw z prędkością 5 m/s (to wyjątkowo szybki żółw).

Zaczynamy pościg.

Dystans pierwotny Achilles przebiegnie w ciągu sekundy.
W czasie sekundy żółw przebiegnie 5 m.
Następny odcinek Achilles przebiegnie w 1/2 s. W tym czasie żółw oddali się od Achillesa o 2,5 m.
Odległość 2,5 m Achilles przebiegnie w czasie 1/4 s. W tym czasie żółw przebiegnie 1,25 m.

Widać już prostą regułę – goniąc żółwia Achilles zużyje czas równy:
1 s+1/2 s+1/4 s+1/8 s+1/16 s + …

Mamy tu do czynienie z sumą nieskończonej liczby składników. Taki obiekt nazywa się w matematyce szeregiem. Ten szczególny szereg jest określany jako szereg geometryczny ponieważ każdy kolejny wyraz tego szeregu jest dwukrotnie mniejszy od poprzedniego.

Suma takiego szeregu jest skończona i wynosi  2 s. Zatem Achilles dogoni żółwia w 2s.

Błędem rozumowania Zenona było zatem założenie, że suma nieskończonej liczby interwałów czasu da czas nieskończony. Zenon nie mógł znać zasad sumowania nieskończonej liczby składników bo takie sumowanie wymaga znajomości metod analizy matematycznej, rozwiniętej wiele wieku później.

Rozważmy teraz drugi wariant pościgu.

Spróbujmy nieco zmodyfikować założenie pościgu. Zachowajmy założenie, że Achilles rusza z większą prędkością niż żółw, ale czasy, w których przebiega kolejne odcinki tworzą ciąg
1 s, 1/2 s, 1/3 s, 1/4 s, 1/5 s, itd.

Czas pościgu Achillesa będzie więc określony następującym szeregiem:
1 s + 1/2 s +1/3 s + 1/4 s + 1/5 s + …

Ten szereg to szereg harmoniczny. Wygląda bardzo podobnie do poprzedniego, ale tym razem nieskończoność pokazuje swoje niezwykłe oblicze.
Mimo, że kolejne wyrazy szeregu są coraz mniejsze suma tego szeregu jest nieskończona co oznacza, że tym razem Achilles nie dogoni żółwia.

Zobaczmy dlaczego tak się stanie.
Dla uproszczenia załóżmy, że kiedy Achilles przebiega kolejny odcinek jego prędkość jest stała.

Tak jak poprzednio zakładamy, że Achilles zaczyna pościg z prędkością 10 m/s a żółw porusza się przez cały czas pościgu z prędkością 5 m/s.

Pierwsze dwa odcinki Achilles przebiega, tak jak poprzednio, z prędkością 10 m/s. Kiedy Achilles pokona drugi odcinek żółw przebędzie odległość 5m/s*1/2 s = 2,5 m. Jeśli Achilles ma tę odległość pokonać w czasie 1/3 s (nieco większym niż poprzednio), to jego prędkość musi być równa 7,5 m/s co oznacza, że uległa ona zmniejszeniu w porównaniu z prędkością startową.

Kontynuacja tych rachunków pokazuje, że kolejne odcinki Achilles będzie przebiegał z coraz mniejszą prędkością:
Odcinek czwarty –  prędkość 6,67 m/s
Odcinek piaty –  prędkość 6,25 m/s
Odcinek szósty –  prędkość 6,00 m/s
itd.

Wyliczenia dla kolejnych odcinków pokazują, że prędkość Achillesa będzie maleć i w nieskończoności zrówna się z prędkością żółwia. I oto mamy wyjaśnienie – Achilles nie dogoni żółwia bo prędkość z jaką biegnie jest coraz mniejsza.

To przypadek maratonu. Żółw maratończyk nie zwalnia a goniący go sprinter Achilles, wprawdzie szybko ruszył, ale w miarę pokonywania dystansu traci siły.

Zwróćmy uwagę, że w obu przypadkach prędkość z jaką biegnie Achilles jest zawsze większa od prędkości żółwia więc wydawać by się mogło, że w obu pościgach Achilles dogoni żółwia. W drugim przypadku intuicja nas jednak zawodzi. Tam gdzie mamy do czynienia z nieskończonością lepiej polegać na matematyce niż na intuicji.

Konkluzja jest więc następująca:

• • w przypadku sprintu – Zenon nie miał racji bo

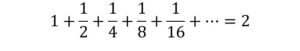
• • w przypadku maratonu – Zenon miał rację bo

***
2022